|
|

|

|
See the GSRM v.2 for a more up-to-date and comprehensive model.
THIS SITE NO LONGER MAINTAINED AND HERE FOR ARCHIVAL PURPOSES.
Global Strain Rate Map Project: Methodology


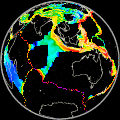
Please give proper credit to results
The methodology adopted to estimate a global strain rate and velocity model
has been presented in
Kreemer et al. [2000a],
but a brief overview
is given here. We make the assumption that the lithosphere in plate boundary
zones behaves as a continuum. This is a reasonable approximation when considering
large-scale deformation for areas that have horizontal dimensions several times
the thickness of the brittle elastic layer (e.g.,
England and McKenzie [1982]).
We adopt the methodology by
Haines and Holt [1993]
to estimate the horizontal
velocity gradient tensor field on a sphere. A bi-cubic Bessel interpolation
is used instead of polynomials, however, to expand a model rotation vector function
that is obtained by a least-squares minimization between model and geodetic
velocities, and model and geologic strain rates. Geological strain rates are
obtained through a summation of Quaternary fault slip rates using a variant of
Kostrov's [1974] formula
[Shen-Tu et al., 1999;
Holt et al., 2000a].
This type of modeling has been presented in numerous papers concerning
regional tectonics in zones of diffuse deformation; e.g., western United States
[Shen-Tu et al., 1999], and central Asia
[Holt et al., 2000a].
A comprehensive overview of the methodology can be found in
Haines et al.[1998],
Holt et al. [2000b], and
Beavan and Haines [2001].
Our model grid is continuous in longitudinal direction and covers the globe
between 80°N and 80°S. Each grid area is 0.6° by 0.5°
in dimension. Whether an area is considered to be deforming or not is based
primarily on seismicity occurrence
(Engdahl et al. [1998]
and the Harvard Centroid Moment Tensor (CMT) catalog
[Dziewonski et al., 1981, 2000]).
All oceanic ridge and transform zones are allowed to deform. Within oceanic
and continental regions of diffuse deformation, where seismicity rates are often
low, the designation of boundaries between deforming and plate-like regions
was often subjective. Therefore, the geometry of deforming regions in this model
should be viewed as approximate. About 25000 grid areas cover the
Earth's deforming regions; all other areas are considered to be rigid. The rigid
areas mimic 25 independent plates and blocks, including a number of relatively
small entities such as the Rivera, Anatolia, Ochotsk, Caroline, Scotia, Sunda,
Tarim, Amuria, and South China plates and blocks, among others.
In this model we currently perform a least-squares fit to 5170 geodetic velocities from
86 different studies (see Introduction for
comparison with earlier GSRM versions). One of the main advantages of the methodology used for this model is that an
unlimited number of geodetic studies may be combined. The original reference
frame of each individual study does not need to be adopted and, in fact, can
be left undefined, a priori, in the inversion; the reference frame is solved
upon fitting geodetic velocities to one self-consistent velocity gradient tensor
field. That is, implicit in our procedure is the assumption that a single rigid
body rotation can be applied to velocity vectors from each individual study
(one rotation vector for each study) such that the model velocity field provides
a ' best-fit' to the observed vectors that have been rotated into
a single model frame of reference. Besides geodetic velocities we
also included Quaternary fault slip rate data from central Asia
[England and Molnar, 1997;
Holt et al., 2000a, and references
therein]. We perform a smoothing of the geologic strain rates over an appropriate length
scale (~50-100 km) such that geodetic and geologic strain rates compliment
each other in reflecting the ongoing horizontal deformation in areas where the
lateral dimension is several times larger than the elastic thickness. As a
consequence of combining these different data sets, the resolution for the global
strain rate model has a lower limit of ~50-100 km.
To accommodate the fact that not all plate boundary zones or areas within one
single plate boundary zone strain with the same magnitude we constrain the magnitude
of the a priori strain rate variance to vary globally. In order to do this all
plate boundary zones are divided into 218 smaller areas. For each of these areas
a value is assigned, depending on the expected magnitude of the strain rate
for the area. For conformity the strain rate variance is chosen from a range
of 4 values, depending on the expected strain rate; the highest a priori variance
value is reserved for the zones that are expected to deform with the highest
strain rate. A priori constraints on the expected lateral variation in strain
rate are especially important for areas in which kinematics are ill-constrained
due to a lack of observed velocities (e.g., Iran, East African Rift Valley,
western Mediterranean, and central America).
For regions that are not densely sampled with geodetic observations, the interpolation
of geodetic velocities can be highly non-unique in describing the regional strain
rate field
[Kreemer et al., 2000b;
Beavan and Haines, 2001]. However,
the design of the strain rate covariance matrix can place a priori constraints
on the style and direction of the model strain rate field. The constraint on
the direction of the principal axes of the model strain rate field involves
an uncertainty of ±10°. Information about the style and direction
of expected strain rate is inferred from the principal axes of the seismic strain
rate field, which is obtained through a
Kostrov [1974]
summation of seismic moment tensors in each grid area. Seismic moment tensors are used only from
shallow events (less or equal 40 km) in the Harvard CMT catalog (January 1977 - November 2002)
and from Pondrelli et al. [2002]
for the Mediterranean (January 1997 - December 2000).
For this purpose all events are weighted equally in the Kostrov summation.
This approach is adopted here, except for areas where Quaternary fault slip
rate data are used to infer geologic strain rate estimates (currently only for
central Asia). It should be noted that only the style and direction of the model
strain rate field is constrained using the direction and style of the seismic
strain rate field, not the magnitude. Also, constraints on the style and direction
of the model strain rate field do not significantly affect the fit of the model
velocities to the observed velocities. Moreover, including constraints on the
style and direction of the model strain rate field results in a solution that
is as consistent as possible with regional seismotectonics, while providing
more stability in the model strain rate field from one grid area to another
[Kreemer et al., 2000b].
References
Beavan, J., and J. Haines, Contemporary horizontal velocity and strain rate fields
of the Pacific-Australian plate boundary zone through New Zealand,
J. Geophys. Res., 106, 741-770, 2001.
Dziewonski, A.M., T.-A. Chou, and J.H. Woodhouse, Determination of earthquake source
parameters from waveform data for studies of global and regional seismicity,
J. Geophys. Res., 86, 2825-2852, 1981.
Dziewonski, A.M., G. Ekström, and N.N. Maternovskaya, Centroid-moment tensor solutions
for July-September, 1999, Phys. Earth Planet. Int., 119, 311-319, 2000.
Engdahl, E.R., R. van der Hilst, and R. Buland, Global teleseismic relocation with improved
travel times and procedures for depth determination, Bull. Seismol. Soc. Am., 88,
722-743, 1998.
England, P.C., and D.P. McKenzie, A thin viscous sheet model for continental deformation,
Geophys. J. Royal Astron. Soc., 70, 295-321, 1982.
England, P.C., and P. Molnar, The field of crustal velocity in Asia calculated from
Quaternary rates of slip on faults, Geophys J. Int., 130, 551-582, 1997.
Haines, A.J., and W.E. Holt, A procedure for obtaining the complete horizontal motions
within zones of distributed deformation from the inversion of strain rate data,
J. Geophys. Res., 98, 12057-12082, 1993.
Haines, A.J., J.A. Jackson, W.E. Holt, and D.C. Agnew, Representing distributed deformation
by continuous velocity fields, Sci. Rept. 98/5, Inst. of Geol. and Nucl. Sci.,
Wellington, New Zealand, 1998.
Holt, W.E., N. Chamot-Rooke, X. LePichon, A.J. Haines, B. Shen-Tu, and J. Ren, The velocity
field in Asia inferred from Quaternary fault slip rates and GPS observations,
J. Geophys. Res., 105, 19185-19210, 2000a.
Holt, W.E., B. Shen-Tu, A.J. Haines, J. Jackson, On the determination of self-consistent
strain rate fields within zones of distributed continental deformation,
in The History and Dynamics of Global Plate Motions, eds. M.A. Richards,
R.G. Gordon, and R.D. van der Hilst, AGU, Washington, D.C., 2000b.
Kostrov V.V., Seismic moment and energy of earthquakes, and seismic flow of rocks,
Izv. Acad. Sci. USSR Phys. Solid Earth, 1, Eng. Transl., 23-44, 1974.
Kreemer, C., J. Haines, W.E. Holt, G. Blewitt, and D. Lavallée, On the determination of
a global strain rate model, Earth Planets Space, 52, 765-770, 2000a.
Kreemer, C., W.E. Holt, S. Goes, and R. Govers, Active deformation in eastern
Indonesia and the Philippines from GPS and seismicity data,
J. Geophys. Res., 105, 663-680, 2000b.
Pondrelli, S., A. Morelli, G. Ekström, S. Mazza, E. Boschi, and A.M. Dziewonski,
European-Mediterranean regional centroid-moment tensors: 1997-2000,
Phys. Earth Planet. Int., 130, 71-101, 2002.
Shen-Tu, B., W.E. Holt, and A.J. Haines, Deformation kinematics in the western United
States determined from Quaternary fault slip rates and recent geodetic data,
J. Geophys. Res., 104, 28927-28955, 1999.
Comments or questions about this page? Send mail to Bill Holt.
(william.holt sunysb.edu or sunysb.edu or
wholt notes.cc.sunysb.edu) notes.cc.sunysb.edu)
|

|

